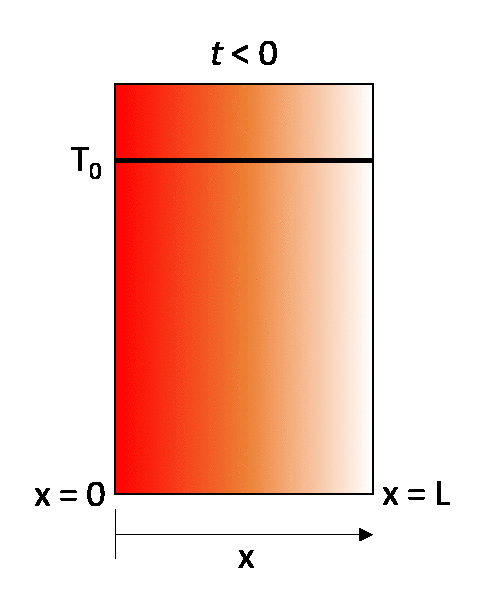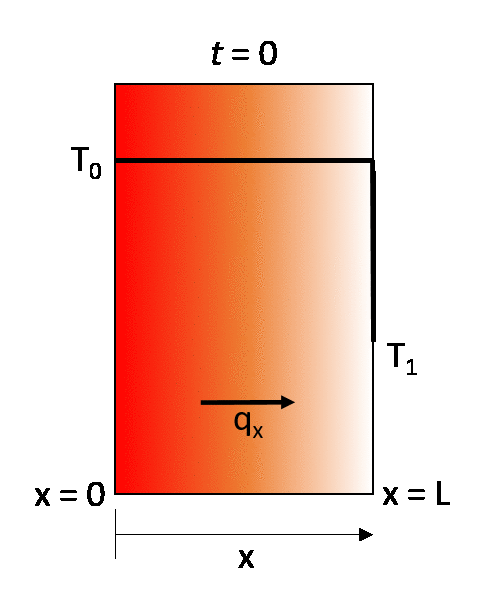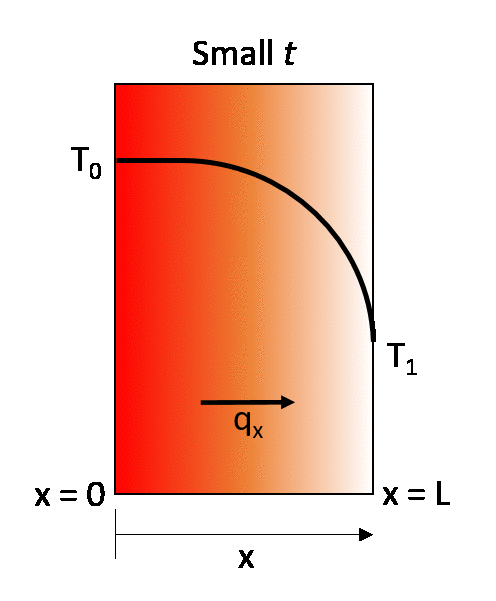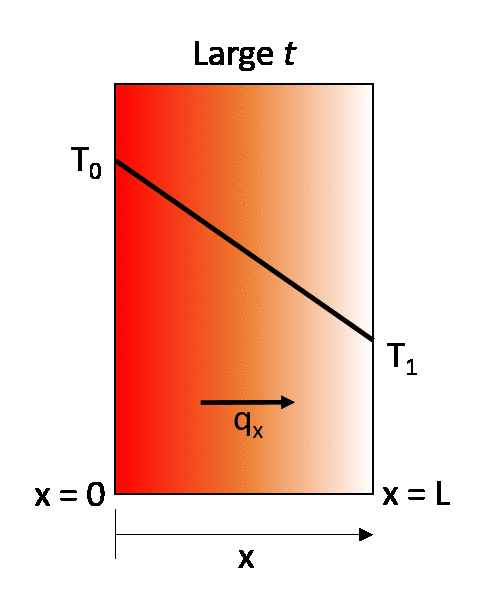Conduction - A118

Conduction
Foundational knowledge article
Document Type	Article
Document Identifier	118
Themes	Thermal management
Relevant Class	Material
Tags	Conductive heating Constitutive equations Governing science Heat transfer Process modelling
Prerequisites	Heat transfer Convection

Introduction

Conduction is a molecular heat transfer mode associated with the microscopic collisions between high energy particles and adjacent lower energy particles causing a redistribution of kinetic energy. Therefore, heat transfer by conduction occurs from regions of higher temperature to regions of lower temperatures.

Scope

This page explains thermal conduction in the context of composites processing and how it differs from other heat transfer mechanisms such as convection. Specifics about the material properties involved in thermal conduction are given in separate pages.

Significance

Conduction is the primary heat transfer mechanism in solid materials. It plays a critical role in composite manufacturing processes, responsible for heat flow in hot press forming platens, tooling and part through-thickness temperature gradients. Both steady-state and transient (non steady-state) conduction are introduced and discussed.

Prerequisites

Recommended documents to review before, or in parallel with this document:

• Heat transfer
• Convection

Conduction overview

Conduction is a molecular heat transfer mode associated with the microscopic collisions between high energy particles and adjacent lower energy particles causing a redistribution of kinetic energy. Therefore, heat transfer by conduction occurs from regions of higher temperature to regions of lower temperatures. It is one of the are three main mechanisms of heat transfer.

Using the classic example of a metal rod being heated over a flame; the heat being transferred from the flame to the rod is considered to be by convection, while the heat transferred along the rod itself is by conduction . Applying this analogy to the composites processing scenario for a laminate curing in an oven or autoclave environment; the hot air transfers heat by convection, while the heat transfer between the tool and laminate part, and within the laminate itself is by conduction.

There are two main properties to heat conduction:

1. Thermal conductivity (\(k\)) (KPC page link)
2. Thermal diffusivity (\(\alpha\)) (KPC page link)

Thermal conduction occurs under two conditions: steady-state, and non-steady or transient conditions.

Steady-state conduction

Steady-state conduction is described empirically by Fourier's Law.

\(\overrightarrow{q}=-k\overrightarrow{\bigtriangledown}T\)

Where,

\(\overrightarrow{q}=\)heat flux

\(k=\) thermal conductivity

\(\overrightarrow{\bigtriangledown}T=\)temperature gradient

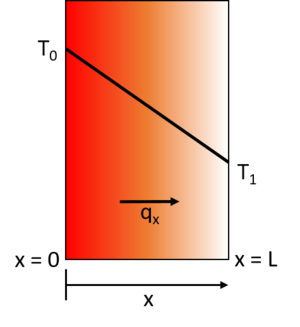
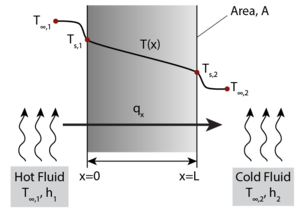
Fourier’s Law provides an empirical description of conduction stating that the heat flux, q, travelling from a region of higher temperature to a region of lower temperature is equal to the product of the temperature gradient, ΔT, between the two regions and the thermal conductivity of the material, k. This means that the energy transport by conduction between two regions increases with the temperature difference between the two regions. A simple one-dimensional heat transfer case by solid-state conduction is shown with a wall exposed on one side to a hot fluid and to a cold fluid on the other side. Under steady state conditions a linear temperature gradient develops inside the wall as heat is transferred from the hot fluid through the solid wall to the cold fluid via conduction.

Linear temperature gradient due to thermal conduction.

For a simple steady-state one-dimensional case, the differential form of Fourier's Law simplifies to:

\(q_x = -k\tfrac{\partial t}{\partial x}\)

Which, if the temperature distribution is linear, becomes:

\(q_x = -k\tfrac{\bigtriangleup T}{\bigtriangleup x}\)

Where \(q_x\) is the heat flux in [W/m²] in the x direction, \(\bigtriangleup T\) is the temperature gradient in [K/m] in the \(x\) direction, and \(k\) is the thermal conductivity of the material in [W/m·K].

In order to understand the 1D steady-state temperature distribution through a part, where one side side is hotter than the other, the differential form of q_x must be substituted into the fundamental energy equation. Take the following example, where an infinitely long wall is heated from one side.

1D steady-state conduction heat transfer, where an infinitely long wall is heated from the left side.

\(-\frac{\partial q}{\partial x}-\frac{\partial q}{\partial y}-\frac{\partial q}{\partial z}+\dot Q_{gen}-\dot Q_{cons}=\rho c_p\frac{\partial T}{\partial t}\)

For this case, the one-dimensional form of the energy equation, with no internal heat generation (\(\dot Q_{gen}\)) or accumulation (\(\dot Q_{cons}\)), i.e., steady state, becomes:

\(- \tfrac{dq_x}{dx}=0\)

Which gives:

\(\tfrac{d}{dx} \Bigl( k \tfrac{dT}{dx} \Bigr) = 0\)

Integrating the above equation and solving for the boundary conditions (i.e. T(0) = T₀ and T(L) = T₁) yields:

\(T_{(x)} = ( T_1 - T_0 ) \tfrac{x}{L} + T_0\)

Under steady-state conditions, the temperature profile increases linearly from T₀ to T₁.

Transient conduction

Transient (non-steady state) conduction involves heat capacity (\(c_p\)), density (\(\rho\)), thermal diffusivity (\(\alpha\)), and a rate term.

The thermal diffusivity is defined as\[\alpha=\frac{k}{\rho c_p}\]

Where,

\(k=\)thermal conductivity [W/m·K]

\(\rho=\)density [kg/m³]

\(c_p=\)specific heat capacity [J/kg·K]

The grouping of terms \(\rho c_p\) is volumetric heat capacity [J/m³·K]

The SI units used of thermal diffusivity are then [m²/s]. Thermal diffusivity varies from low values of about 0.1 10^-6 m²/s to high values of about 1000 10^-6 m²/s. When the thermal conditions around a material changes, a material with a high thermal diffusivity will reach thermal equilibrium faster than a material with a lower thermal diffusivity.

Thermal diffusivities of some common materials used in composite manufacturing are given in the following table:

Material	Thermal Diffusivity [10-6 m2/s]
Aluminum	68.9
Steel	14.2
Invar	2.7
Carbon-Epoxy Composite	0.5

The earlier described steady-state example can be turned into a transient state conduction case by considering that the same wall is initially at a temperature T_0. throughout, and then that at time t = 0 its right-hand wall is suddenly brought to the temperature T₁. As time proceeds, the through-thickness temperature of the wall changes as heat flows in or out of the wall until eventually the linear steady-state distribution described in the previous section is achieved.

1D-transient conduction where the right-hand wall is suddenly decreased to temperature T₁

For this case, the one-dimensional form of the energy equation becomes\[-\frac{dq_x}{dx}=\rho c_p\frac{\partial T}{\partial t}\]

Therefore,

\(\frac{d}{dx}\Biggl(k\frac{dT}{dx}\Biggr)=\rho c_p\frac{\partial T}{\partial t}\)

Which gives\[\alpha\frac{d^2T}{dx^2}=\frac{\partial T}{\partial t}\]

Where \(\alpha\) is the thermal diffusivity in [m²/s].

The rate of temperature change, and consequently the time to reach thermal equilibrium, therefore depends on the thermal diffusivity of the material.

For a composite laminate curing in an autoclave or oven, where the moving air is acting as a convective heat transfer boundary condition, graphical Heisler charts can be used to look up an approximate solution to the transient conductivity equation for the internal temperature profile of the laminate. Modern technology also allows an exact solution to be obtained using a number of available math or finite element software packages . Alternatively, a simplified closed-form approximation developed by Rasekh et al. can also be used. For more information regarding using this approximation, please see the paper by Rasekh et al. here.

Related pages

Page type	Links
Introduction to Composites Articles
Foundational Knowledge Articles	Conduction - A118 Convection - A106 Glass transition temperature (Tg) - A210 Heat of reaction - A114 Heat transfer - A132 Materials science - A235 Processing science - A151 Thermal behaviour - A232 Thermal conductivity - A116 Thermal diffusivity - A143 Viscosity (resin) - A203
Foundational Knowledge Method Documents
Foundational Knowledge Worked Examples
Systems Knowledge Articles
Systems Knowledge Method Documents
Systems Knowledge Worked Examples
Systems Catalogue Articles
Systems Catalogue Objects – Material
Systems Catalogue Objects – Shape
Systems Catalogue Objects – Tooling and consumables
Systems Catalogue Objects – Equipment	Rheometer - A357
Practice Documents	Practice for developing a thermal transformation process step - P105
Case Studies	Troubleshooting of room temperature processes for large recreational and industrial parts - C100
Perspectives Articles	Case Study: Optimizing a Press Moulding Process - A324 Composite materials engineering webinar session 4 - Thermal management and resin cure - A123 Composites Process Simulation: A Review of the State of the Art for Product Development - A283 Dr. Anoush Poursartip's cdmHUB global composites expert webinar - A136 Fabric Forming: how it affects design and processing, and how simulation can address this - A310 Heat Transfer in Composites Processing - A321 Interview with Prof. Kevin Potter - A134 Simulation models for rapid liquid composite molding - A333.0

References

About	Help

Engineered materials (designed to have specific properties) made from two or more constituent materials with different physical or chemical properties. The constituents remain separate and distinct on a macroscopic level within the finished structure.

A quantitative measure of how a material will respond to transient thermal conditions. It is defined as the ratio of thermal conductivity to the volumetric heat capacity of the material (density times the specific heat capacity).

Materials with large thermal diffusivity have a high thermal conductivity relative to their capacity to store energy (heat capacity) and will rapidly distribute the thermal energy throughout its volume and rapidly change temperature to reach the new equilibrium temperature.

Materials with small thermal diffusivity have a low thermal conductivity relative to their capacity to store energy (heat capacity) and will have a sluggish temperature response to a change in thermal conditions (large temperature lag). This is because it takes more energy per unit volume to change the temperature, and the low thermal conductivity means it takes longer to distribute the thermal energy throughout its volume.