| Composite properties
|
| Foundational knowledge article
|

|
| Document Type
|
Article
|
| Document Identifier
|
214
|
| Themes
|
|
| Tags
|
|
This page provides links to composite properties. In the Knowledge in Practice Centre (KPC), composite properties are defined as properties that describe the combined or homogenized composite material.
For a composite, its properties are influenced by a combination from both the reinforcement and matrix material constituents.
Below are composite property pages found in the KPC:
Heat of reaction (composite)[edit | edit source]
The heat of reaction HR of a composite material is dependent on its matrix component. As the heat of reaction is referenced to the total weight of the material, for a composite it is proportional to the weight fraction of the resin matrix.
HR(composite)=(massfractionresin)×HR(resin)
KPC page for heat of reaction (composite) coming soon.
Degree of cure (composite)[edit | edit source]
While degree of cure (DOC) is a description of the matrix state, there are several points of discussion when considering the DOC of a composite.
Prepreg DOC
The as-received state of the matrix in a prepreg material is not 0 (fully unreacted). As a byproduct of the prepregging process, the matrix has already partially begun its reaction process. However, this initial DOC value is generally low, often assumed to be 0 or only a slightly advanced value, if proper storage and handling has been observed in its thermal history, that prevent the thermoset resin matrix reaction from having advanced substantially.
Cure kinetic changes
With the addition of the composite reinforcement material to the resin matrix, compared to considering only the matrix on its own, changes to the resin cure kinetics can occur and may result in a different degree of cure than expected.
The simple presence of the reinforcement material itself alters the thermal behaviour of the material system; influencing both the heat energy transported to and away from the curing resin – potentially altering the cure kinetics behaviour of the resin system.
The reinforcement material itself may also become directly involved in the resin reaction. Even inert reinforcement materials, may have an unintended influence. For example, reinforcement fibres are typically produced with a proprietary sizing coating that can interact with the resin curing reaction (as the sizing material is generally unknown, this is usually determined experimentally).
KPC page for degree of cure (composite) coming soon.
Crystallization (composite)[edit | edit source]
The presence of the reinforcement material can influence the crystallization behaviour of a thermoplastic matrix in the combined composite material. The reinforcement material has both the potential to both promote and hinder the crystallization process.
Promoting crystallization, reinforcement can act as nucleation sites for the initiation of the crystallization process. Hindering the crystallization process, the reinforcement can act as a volumetric physical constraint, limiting the crystal structure growth.
KPC page for crystallization (composite) coming soon.
Specific heat capacity (composite)[edit | edit source]
The heat capacity of a composite material is a combination of the heat capacity of both the reinforcement and matrix constituents. A rule of mixtures approach is appropriate, where the combined heat capacity is proportional to the amount of reinforcement and matrix.
Click here to visit the general Heat Capacity KPC page.
Thermal conductivity (composite)[edit | edit source]
The thermal conductivity of a composite material is a combination of the thermal conductivity of both the reinforcement and matrix constituents.
When the thermal conductivity of both the reinforcement and matrix (generally assumed the case for polymer matrices) constituents is the same in all directions, a rule a rule of mixtures approach is appropriate. Here, the combined thermal conductivity of the composite material is proportional to the amount of reinforcement and matrix.
For composites containing reinforcements where the thermal properties vary greatly on direction (e.g. fibrous reinforcement), the combined thermal conductivity is dependent on the direction of heat flow. In the fibre in-plane direction, a rule of mixtures approach is appropriate. However, in the transverse fibre direction, other approaches to determine the resulting thermal conductivity of the composite material must be applied.
Click here to visit the general thermal conductivity KPC page (modelling of the thermal conductivity for combined composite materials is introduced).
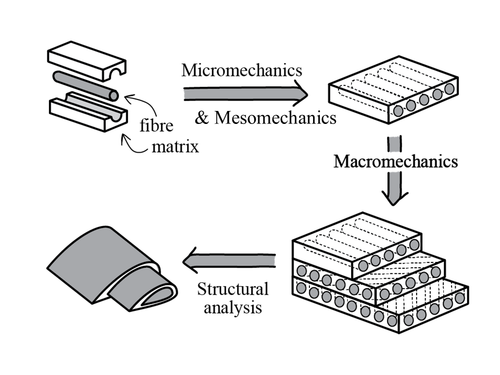
The mechanical analysis of composite materials spans multiple size-scales. Analysis involves scales ranging from the small micro- and mesoscale, up to the larger macro-, and structural scale.
The mechanics of composite materials is inherently complex as it entails the interaction between its multiple different materials. Prediction of the composite material’s mechanical behaviour involves analysis at several size scales: micro-, mes-, and macro- mechanics.
Link to Micro-Mechanics page
The micro-mechanics page guides the user through coordinate system conventions, plane stress effects and the rule of mixtures at level 1.
For level 2 the page goes in to detail about Hooke's law for different loading scenarios, before continuing and building the stiffness and compliance matrices leading to the transformation matrix for angled laminas. Further moving on to describing global engineering constants and the coupling terms in the matrix. Both levels also describe how global engineering constants change with angles of the fibers relative to the loading direction.
Link to Macro-Mechanics page
Macro-mechanics and laminate plate theory allows for the determination of properties of a composite at the laminate level. This is when lamina or plies are put together to form a composite structure and the interactions between them.
Level 1 describes beam theory and how stress is distributed through the beam, before continuing on to describe laminate code conventions and the coupling of loads and their effects.
Level 2 Expands on beam theory and the derivation of the strain equation. Furthermore, the page goes in to detail of stiffness matrices and stress analysis through the ABD matrix and its derivation, leading into plate theory. The coupling of loads in a plate are described using matrix terms and how to balance them. Lastly, a systematic approach to determining engineering constants and stress analysis is presented.
Link to Fatigue Limits page
Fatigue limit is when a material is cycled between two loads until failure. This is due to crack forming during cycling and the further propagation of the cracks until a critical length is reached and the material fails. It is a topic widely studied in metals and is an important aspect when designing with any material. This page will discuss the fundamentals of fatigue limits, before discussing the specific considerations for composite materials.
While it is common practice to isolate and examine the viscosity of the resin matrix component on its own, it is important to consider the influence of the other composite constituent materials when the entire combined system of the matrix and the reinforcement materials are considered together as a whole viscous material.
When examining the composite material system as a whole, the addition of the reinforcement fibres has an enormous influence viscoelastic response of the material system. The fibres are able to resist shear deformation in proportion to the shear modulus of the fibre bed due to the waviness of the fibres, with this effect being higher for high volume fraction composites [1]. The fibre bed’s ability to absorb and dissipate the applied shear forces acts to essentially “thicken” the viscous behavioural response of the fibre/resin composite material. As a result, the effective viscosity of the composite material is much higher when compared to examining solely the resin viscosity on its own.
Measured increases in G’’ of several orders of magnitude have been shown in the literature when comparing prepreg viscoelastic response in comparison to neat resin (same resin system) response in oscillatory rheometer tests [1]. The measured parameter G’’ from oscillatory rheometer tests characterizes viscous portion of a material's viscoelastic behaviour [2].
At low shear ratesμ=η′=G″
Where,
\eta' = Dynamic viscosity
G'' = Viscous modulus
\omega = Angular frequency
KPC page for viscosity (composite) coming soon.
For methods to obtain material property values, please see the Foundational Methods Documents page:
Link to Foundational Method Documents page
Explore this area further
Related pages
| Page type
|
Links
|
| Introduction to Composites Articles
|
|
| Foundational Knowledge Articles
|
|
| Foundational Knowledge Method Documents
|
|
| Foundational Knowledge Worked Examples
|
|
| Systems Knowledge Articles
|
|
| Systems Knowledge Method Documents
|
|
| Systems Knowledge Worked Examples
|
|
| Systems Catalogue Articles
|
|
| Systems Catalogue Objects – Material
|
|
| Systems Catalogue Objects – Shape
|
|
| Systems Catalogue Objects – Tooling and consumables
|
|
| Systems Catalogue Objects – Equipment
|
|
| Practice Documents
|
|
| Case Studies
|
|
| Perspectives Articles
|
|







