Fatigue Limits - A330

 

Fatigue Limits
Foundational knowledge article
Document Type	Article
Document Identifier	330
Tags	Mechanical properties
Prerequisites	Composite properties

Introduction

Fatigue limit refers to the number of loading cycles a material can experience before failure. Failure is typically caused by a crack that incrementally grows during cyclic loading until reaching a critical length, at which point the material fails. It is a topic widely studied in metals and an important aspect when designing with any material. This page will discuss the fundamentals of fatigue limits, before discussing the specific considerations for composite materials.

Fundamentals

To display the fatigue limit of a material a relation between the applied stress and the growth of a crack needs to be established. The stress intensity factor \(∆K\) is the difference between the max and min load applied in a cycle. The material’s ability to resist crack growth is given by the crack growth rate per loading cycle: \[\frac{dc}{dN}\]

For mid-range values of \(∆K\), crack growth rate usually conforms to the Paris-Erdogan relation: \[\frac{d c}{d N}=\beta(\Delta K)^n\] Where β is a constant and when the function is plotted on a log scale, the mid-range values of \(∆K\) give a straight line with slope \(n\). At the extremes, for low \(∆K\) there will be no crack propagation, referred to as \(\Delta K_{t h}\). At high \(∆K\) values the plot will spike showing an area of rapid crack growth and failure of the material. See graph below for an example plot.

Example of Paris-Erdogan Plot Showing dc/dN vs deltaK with Lower Limit with No Propagation and Upper Limit with Crack Propagation

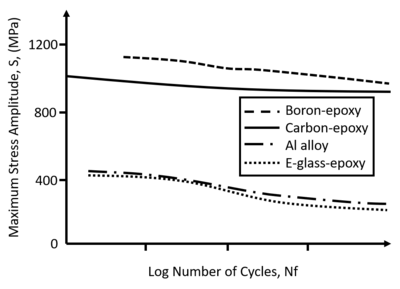
This relation can also be shown in terms of numbers of cycles to failure, \(N_{f}\), as a function of the stress amplitude, \(S\), commonly known as an \(S-N\) curve. Generally, this plot will show that a material can fail with a low number of cycles when the stress is high and visa versa. This plot also illustrates regimes where the material will not fail, even at very high numbers of cycles. Indicating a stress intensity below \(\Delta K_{t h}\). See the chart below for examples of the various fatigue limits for different composites and an aluminum alloy. Note how the glass fibre-epoxy compares well to the metal and the carbon and boron composites show a much higher tolerance for high stress cyclic loading.

Examples of the Fatigue Limits for Various Composites Compared to an Aluminum Alloy.

Crack Propagation in Composites

Fatigue in composites manifests in cracks occurring and propagating through the matrix and along the interfaces of fiber and matrix. This is strongly dependent on how the stress distribution is affected by the fibers. The failure strain of the matrix is also an important factor to consider. For continuous fiber composites it is common for microcracks to occur throughout the material. This is mitigated by fibers bridging across the cracks in the matrix and reducing the intensity factor of the crack.

Composites, in general, perform well in preventing cracks to propagate in cyclical loading. This is due to a full elastic recovery of the fibers when they are unloaded, meaning that the \(\Delta K_{t h}\) can be higher than other materials. High-strength fibers, such as boron and carbon, show excellent fatigue properties as they are able to withstand the high loads seen at microcracks. On the other hand, even though glass fibers also show elastic recovery, they have a lower stiffness. Leading to an inability to sufficiently bridge microcracks in the matrix and thus to higher stresses and strains in the matrix and a lower fatigue limit.

Fiber Direction

Much like the strength properties of fiber composites, loading along the axis of the fibers will give a high fatigue limit. Cyclic loading transversely to the fibers give a much lower fatigue limit as the fibers are not able to bridge the cracks. This is also seen in woven fabric and quasi-isotropic laminates. Even with the issues of axial loading, composites compare well to fatigue limits of metal.

In woven and crossply laminates, the failure of the material is still dependent on the 0° direction plies, such that, during cyclic loading as cracks are forming, the load is transferred to the 0° fibers. Until the matrix has degraded too far and is not able to transfer any loads.

Compression

Composites may be sensitive to different types of loading that may affect the fatigue limit. Specifically, sensitivity to compressive stresses due to fiber buckling. This leads to damage in the fibers, the matrix and the interface between the two. This presents an additional source of cracks as the material is loaded and an additional cracking site, the fibers. With the fibers damaged, there is no chance of the cracks successfully being bridged by the fiber, leading to a low fatigue limit for stresses of an unproblematic magnitude if loaded in tension instead.

Aramid fibers are particularly sensitive to this effect due to their poor compression resistance properties. A mitigating strategy is to have larger diameter fibers to attempt to resist buckling.

Cycle Frequency

For metals, the frequency of loading usually has a low effect. For composites, however, higher frequencies can promote faster failure. This is due to two main reasons, polymer matrix response and heat buildup. Firstly, the viscoelastic response of the polymer during high strain rates causes matrix damage as the material has little time for creep and strength relaxation. Secondly, high frequencies will heat up the material and due to low thermal conductivity in polymers, the heat will dissipate slowly. This effect is exaggerated in glass and aramid fibers since they also have a low thermal conductivity. So, when the polymer heats up it is more prone to failure.

References

About	Help

Engineered materials (designed to have specific properties) made from two or more constituent materials with different physical or chemical properties. The constituents remain separate and distinct on a macroscopic level within the finished structure.

The continuous material phase that binds the reinforcement together, maintains shape, transfers load, protects the reinforcement from environment and damage, and provides the composite support in compression.

Desirable characteristics:

• Moisture/chemical resistance
• Low density
• Processability