Elastic moduli (composite) - A245
| Elastic moduli (composite) | |
|---|---|
| Foundational knowledge article | |
| |
| Document Type | Article |
| Document Identifier | 245 |
| Themes | |
| Tags | |
Overview[edit | edit source]
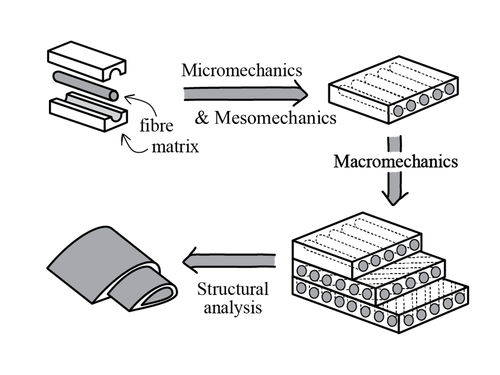
The mechanics of composite materials is inherently complex as it entails the interaction between its multiple different materials. Prediction of the composite material’s mechanical behaviour involves analysis at several size scales: micro-, mes-, and macro- mechanics.
Micro and mesomechanics allows for the determination of elastic moduli at the ply or lamina level for a composite material.
To learn about the mechanics of composites, beyond the scope of content on this page:
- Click here to view the KPC AIM Event: Composite materials engineering webinar session 8 - Mechanics of composites - Part 1: Lamina level
- Click here to view the KPC AIM Event: Composite materials engineering webinar session 9 - Mechanics of composites - Part 2: Laminate level
- Click here to view the KPC AIM Event: Parameters for Structural Analysis of Composites
Direction dependence[edit | edit source]
A combination of both the aspect ratio of the reinforcement and its respective orientation, and the stacking laminate structure that is typically used to construct composite structures gives composite materials a strong anisotropic nature (dependence on the direction of load). As an outcome, a composite’s various elastic moduli are also very directionally dependent.
A common ‘dialect’ has been developed among those who perform design and analysis with composite materials, and is illustrated below.
1 - fibre direction
2 - transverse fibre direction, in-plane
3 - out-of-plane
u, v, w – displacements in 1, 2, 3 directions respectively
At the lamina level (a single laminate ply) or if all the reinforcement material is continuous and running in a single direction, a rule of mixtures approach can be applied when doing analysis of the various elastic moduli. In this approach, an approximation of the composite properties is obtained by using volume-weighted averages of the various composite constituents.
Tensile Young's Modulus[edit | edit source]
Continuous unidirectional fibre reinforcement, fibre direction (1-direction):
\(E_1={E_f}{V_f}+{E_m}{V_m}\)
Where,
\(E_f = \) Fibre tensile Young's modulus
\(V_f = \) Fibre volume fraction
\(E_m = \) Matrix tensile Young's modulus
\(V_m = \) Matrix volume fraction
Continuous unidirectional fibre reinforcement, transverse fibre direction (2-direction):
\(\frac{1}{E_2}=\frac{1}{E_f}{V_f}+\frac{1}{E_m}{V_m}\)
Where,
\(E_f = \) Fibre tensile Young's modulus
\(V_f = \) Fibre volume fraction
\(E_m = \) Matrix tensile Young's modulus
\(V_m = \) Matrix volume fraction
Shear Modulus[edit | edit source]
Continuous unidirectional fibre reinforcement, in-plane (1,2-direction):
\(\frac{1}{G_{12}}=\frac{1}{G_f}{V_f}+\frac{1}{G_m}{V_m}\)
Where,
\(G_f = \) Fibre shear modulus
\(V_f = \) Fibre volume fraction
\(G_m = \) Matrix shear modulus
\(V_m = \) Matrix volume fraction
Mechanical Testing (External Links)[edit | edit source]
- CMH-17 Composite Materials Handbook
- ASTM Testing Standards (ASTM International)
- Suppliers of Advanced Composite Materials Association (SACMA)
Related pages
| Page type | Links |
|---|---|
| Introduction to Composites Articles | |
| Foundational Knowledge Articles | |
| Foundational Knowledge Method Documents | |
| Foundational Knowledge Worked Examples | |
| Systems Knowledge Articles | |
| Systems Knowledge Method Documents | |
| Systems Knowledge Worked Examples | |
| Systems Catalogue Articles | |
| Systems Catalogue Objects – Material | |
| Systems Catalogue Objects – Shape | |
| Systems Catalogue Objects – Tooling and consumables | |
| Systems Catalogue Objects – Equipment | |
| Practice Documents | |
| Case Studies | |
| Perspectives Articles |
 |
 |
| About | Help |
Welcome
Welcome to the CKN Knowledge in Practice Centre (KPC). The KPC is a resource for learning and applying scientific knowledge to the practice of composites manufacturing. As you navigate around the KPC, refer back to the information on this right-hand pane as a resource for understanding the intricacies of composites processing and why the KPC is laid out in the way that it is. The following video explains the KPC approach:
Understanding Composites Processing
The Knowledge in Practice Centre (KPC) is centered around a structured method of thinking about composite material manufacturing. From the top down, the heirarchy consists of:
- The factory
- Factory cells and/or the factory layout
- Process steps (embodied in the factory process flow) consisting of:
The way that the material, shape, tooling & consumables and equipment (abbreviated as MSTE) interact with each other during a process step is critical to the outcome of the manufacturing step, and ultimately critical to the quality of the finished part. The interactions between MSTE during a process step can be numerous and complex, but the Knowledge in Practice Centre aims to make you aware of these interactions, understand how one parameter affects another, and understand how to analyze the problem using a systems based approach. Using this approach, the factory can then be developed with a complete understanding and control of all interactions.
Interrelationship of Function, Shape, Material & Process
Design for manufacturing is critical to ensuring the producibility of a part. Trouble arises when it is considered too late or not at all in the design process. Conversely, process design (controlling the interactions between shape, material, tooling & consumables and equipment to achieve a desired outcome) must always consider the shape and material of the part. Ashby has developed and popularized the approach linking design (function) to the choice of material and shape, which influence the process selected and vice versa, as shown below:
Within the Knowledge in Practice Centre the same methodology is applied but the process is more fully defined by also explicitly calling out the equipment and tooling & consumables. Note that in common usage, a process which consists of many steps can be arbitrarily defined by just one step, e.g. "spray-up". Though convenient, this can be misleading.
Workflows
The KPC's Practice and Case Study volumes consist of three types of workflows:
- Development - Analyzing the interactions between MSTE in the process steps to make decisions on processing parameters and understanding how the process steps and factory cells fit within the factory.
- Troubleshooting - Guiding you to possible causes of processing issues affecting either cost, rate or quality and directing you to the most appropriate development workflow to improve the process
- Optimization - An expansion on the development workflows where a larger number of options are considered to achieve the best mixture of cost, rate & quality for your application.
