Effect of tooling in a thermal management system - A142

Effect of tooling in a thermal management system
Systems knowledge article
Document Type	Article
Document Identifier	142
Themes	Thermal management
Relevant Classes	Tooling and consumables
Tags	Consumables System control Tooling Thermal properties Thermal transformation Tooling parameters Thermal management interaction
Prerequisites	Degree of cure Heat of reaction Heat transfer Specific heat capacity System interactions Thermal conductivity Thermal diffusivity Thermal and cure/crystallization management (TM)

Introduction

In processing of composites, the tooling and consumables constitute at least one boundary with respect to the part. In order for heat to transfer to and from the part, it must pass through the tooling/consumables. Hence, the parameters of the tooling can significantly impact the thermal response of the part. This includes the initial temperature of the tooling, which in turn impacts the initial part temperature. Since the system response is time-dependent, if the initial temperature of the tool-part assembly is not as expected, then its thermal response will similarly be unexpected.

Scope

This article discusses the impact tooling has on the part thermal response. The effect of various tooling parameters are investigated from a thermal management perspective. The page links out to foundational knowledge content and brings in physics-based simulation to demonstrate the impact of tooling in a thermal system. While the content presented here is applicable to all thermal management factory cells, the focus of this page is on the thermal transformation cell as that is the predominant cell associated with thermal management.

Significance

Tools are typically designed to support and provide shape to the part following well-defined mechanical requirements. However, it is also important that manufacturers consider thermal management specifications for tools. While the material(s), part(s), and even equipment parameters may be constrained, the tooling parameters are often not specified. Therefore, there is room to tailor the parameters of the tooling and consumables in order to achieve the necessary part thermal history. Small changes to the tooling may provide significant changes to the thermal response of the system. This, in turn, can affect the part temperature, gel time, and its final degree of cure (DOC).

Prerequisites

Recommended documents to review before, or in parallel, with this document:

• Degree of cure
• Heat of reaction
• Heat transfer
• Specific heat capacity
• Thermal conductivity
• Thermal diffusivity
• Thermal management
• System interactions
• Tooling and consumables (system class)

Analysis

There are a number of tooling parameters that may affect the outcome of the part in a thermal management system. The most significant are the tooling material, thickness, and initial temperature. However, the configuration of the tool should also be considered. Whether or not the tool has a substructure is important for the tool-side heat transfer coefficient (HTC), and the shape of the tool will influence airflow and local HTC values.

Thermal response of three different tools following a 5°C/min heating rate to 100°C. See the tooling survey section below for more details.

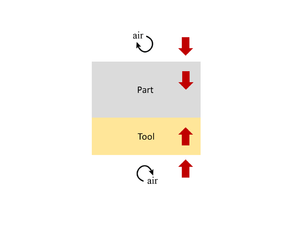
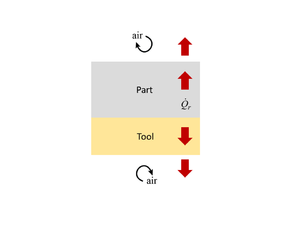
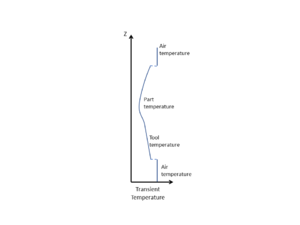
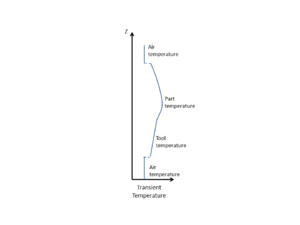
In regards to thermal management, the tool can be generalized as affecting the system in two ways; either behaving as a heat source, or a heat sink with respect to the part. The former occurs during a heat up scenario, in which heat must flow through the tool into the part. Initially, the tool and part are at the same temperature. Typically, as heat is added to the system, the tool heats up first which in turn transfers heat to the part, thus acting as a heat source. Both tool and part add thermal resistance to the system which results in a discrepancy between the part temperature and the applied temperature, known as thermal lag. In some cases, the tool may be the component applying heat to the system, in which case the tool still acts as a heat source, but the initial temperature of the part and tool are not the same. The second effect of tooling occurs during polymerization of the resin, when the material "exotherms". Here, additional heat is added to the system from the part. The part temperature is now greater than the tool temperature, meaning heat must escape through the tool. The tool behaves as a heat sink. In both cases, the tool acts as a medium of heat transfer. In the first case, the goal is to transfer heat to the part, whereas in the latter case the goal is to transfer heat away from the part. For a room temperature process, only the latter case need be considered, since there is no "heat up" stage. Conversely, both cases must be considered when processing at elevated temperatures.

In many cases, a 1D representation of the heat flow is adequate. Typically, the in-plane dimensions of composite materials are much larger than the their thickness. As a result, in-plane heat transfer can be ignored for most cases. This is a conservative approximation and does not always hold true. For example, highly conductive tooling materials (such as aluminum) may affect the validity of a 1D approximation. That said, the examples provided here are based on a 1D assessment.

Heat-up	Exotherm
Schematic showing heat flow through tool into the part during heat up	Schematic showing heat flow through tool from the part during resin polymerization
Temperature profile across system components during heat up	Temperature profile across system components during exotherm

Heat transfer into and out of the part occurs by conduction through the tool-part assembly. It is at the interface between the equipment and tool, and equipment and part, where convection takes place (if in a convective heating system). Recall that the ET interaction serves as the boundary conditions for the part. If the temperature across the upper and lower tooling surface (or part surface if not surrounded by tooling/consumables) is known, then the temperature within the part can be approximated using the 1D form of the heat balance equation, as shown below.

\(\frac{\partial}{\partial t}(\rho C_pT)=\frac{\partial}{\partial z}\Bigl(k_{zz}\frac{\partial T}{\partial z}\Bigr)+\dot{Q}_{r}\) 1D form of the heat transfer equation, where:<br />\(t\) = time,<br />\(\rho\) = density,<br />\(C_p\) = specific heat capacity,<br />\(T\) = temperature,<br />\(z\) = through-thickness distance (z direction),<br />\(k_{zz}\) = thermal conductivity in z direction, and<br />\(\dot{Q}_{r}\) = rate of energy given off by material during exotherm.

Where,

\(\dot Q_r = \frac{d\alpha}{dt}(1-V_f)\rho_r H_R\) Internal heat generation during polymerization (exotherm), where:<br />\(\dot{Q}_{r}\) = rate of energy given off by material,<br />\(\alpha\) = degree of cure,<br />\(t\) = time,<br />\(V_f\) = fibre volume fraction,<br />\(\rho_r\) = resin density, and<br />\(H_R\) = heat of reaction of resin

In order to understand the surface temperature of the tooling, it must be accurately measured or the heat transfer coefficient (HTC) of the equipment must be known. This is often a source of uncertainty in composites process modelling. To perform a thermal assessment of a part/tool or measure the HTC refer to the following pages:

• How to perform an experimental thermal profile
• How to perform a numerical thermal profile
• How to experimentally determine the HTC
• How to back calculate the HTC using simulation

Effect of geometry

Tooling thickness

In a thermal system, the tooling may act as a heat source or sink with respect to the part. The more thermally massive the tool, the more energy (heat) is required to raise its temperature. Since the tool is adjacent to the part, this directly affects the part temperature. For room temperature cure applications, there is no external heat added to the system. Rather, it is the exothermic polymerization reaction of the thermosetting material that contributes heat to the system and advances cure. If the heat that is given off is not managed properly, the part may thermally degrade (i.e. burn). One way to manage the part temperature is to use the tool as a heat sink. As the part gives off heat, the tool will absorb it. Again, the more thermally massive the tool, the more heat it will absorb. In other words, a thicker tool will absorb more heat from the part than a thin tool. This can be observed in left image in the figure below. The temperature of the part and tool start at 20°C. As polymerization kicks off, the part gives off an enormous amount of heat. With nothing to absorb the heat, a 10mm glass-polyester laminate can experience temperatures in excess of 200°C. As tooling thickness is increased, however, the maximum temperature is greatly reduced. That is not to say that the exotherm should be completely reduced, as often material systems, especially those cured at room temperature, make use of this additional heat. Polyester resins for example are typically cured at room temperature and utilize the heat generated from their polymerization reaction to advance the cure. On that note, while increasing tooling thickness reduces the maximum part temperature, it increases the time at which the part remains at elevated temperature. Just as increasing tooling thickness delays the heat up response of the part, due to the tool absorbing more heat, it also delays the cool down response of the part, as now more heat must be given off. The "no tool" case, for example, heats up relatively fast above 200°C and then cools relatively quick as well. Conversely, with a 30mm tool, the part heats up much slower to below 50°C, but remains at an elevated temperature for much longer This may be beneficial in reaching an appropriate degree of cure, or detrimental if at too high a temperature for too long. Achieving the appropriate thermal history for polyesters often boils down to managing this exothermic heat. Altering tooling thickness to achieve the appropriate thermal response of the part is not only an effective thermal management strategy for room temperature cures but also for high temperature cures.

At elevated temperatures, a thicker tool will result in a greater thermal lag between the part and environmental temperature, since more energy is spent heating the larger tool. Note the patterns observed in the right image in the figure below. In this scenario a carbon epoxy laminate is placed on an aluminum tool with varying thickness. The laminate is exposed to air on its top surface. Both part and tool are subject to a heat transfer coefficient indicative of that in a convection oven (20 W/m²k). With no tool present, the part temperature follows the applied temperature relatively closely. Eventually the exothermic polymerization reaction of the epoxy adds additional heat to the system and the part experiences a significant overshoot above the environmental temperature. In contrast, a tool thickness of 30mm results in a much slower thermal response of the part, but completely mitigates the exothermic overshoot. Tooling thickness does not only affect the rate in which the part is heated, but also in drawing heat from the part. That is why at a tooling thickness of 30mm, the exothermic nature of the part is subsided, because the heat released from the part is drawn into the tool. While the temperature overshoot may not be desirable, combating the effect with a large tool results in a longer cure cycle, since the part takes longer to reach the intended temperature of 180°C. This is a common optimization problem faced by manufacturers; meeting the intended temperature specifications with the shortest possible cure cycle. Moreover, just as in the room temperature case, the time it take for the part to cool down is in increased for thicker tools. If the tool is not thick enough to reduce the exotherm below the max allowable temperature, then it may contribute to holding the part above the max temperature for an extending period of time; an undesirable effect.

In order for a material system to achieve a high degree of cure, a sufficient amount of energy (heat) must be put into advancing the polymerization reaction. This is why for the room temperature scenario, a higher degree of cure is associated with a higher maximum temperature, because more thermal energy is available to advance the cure. As the polymerization reaction progresses, if the temperature does not reach the minimum energy threshold to continue advancing the cure, then the degree of cure will stabilize. Therefore, a thinner tool which results in a higher maximum temperature, advances the degree of cure further and at a faster rate. That said, in the case of the high-temperature processing scenario, while the cure rate may be different, the final degree of cure tends to the same value despite the differences in maximum temperature. This is because, regardless of tooling thickness, the system will eventually stabilize at the intended hold temperature of 180°C, which is high enough to raise the DOC to the final value shown for that material system. Conversely, at room temperature processing, once the part temperature has peaked, it will decrease in temperature until it eventually stabilizes at 20°C again. While the part temperature may be high enough to advance cure during the exotherm, if that temperature is not maintained then the cure reaction will eventually stop progressing as the part cools. Recall also that, in many cases, the amount of energy needed to advance polymerization to high DOC levels becomes significant. This is why the high temperature carbon-epoxy does not ever achieve a DOC of 1 under the given conditions, no matter the tooling thickness.

While a thinner tool may result in a higher DOC or a faster cure cycle, one should be wary to make the assumption that thinner tools are therefore better. As shown in the part temperature graphs, the maximum temperature can be quite high and, in many cases, above that of the material's degradation temperature. Hence, while a high degree of cure is desired, tooling thickness should be carefully chosen so not to degrade the part in achieving this goal.

Thermal response of two material systems on an aluminum tool of varying thickness. Left: Glass-polyester composite cured at room temperature (20°C). Right: Carbon-epoxy composite cured at 180°C with a ramp rate of 3°C/min in an oven.

Room temperature (20°C)	High temperature (3°C/min to 180°C)

Tool surface thickness is not always consistent. One potential cause of this type of thickness variation is during tool construction, plates were welded and then machined to shape, see image below. As a result, thicker surfaces can lag thinner areas on the surface.

side view of invar tool showing uneven face sheet thickness

Tooling configuration

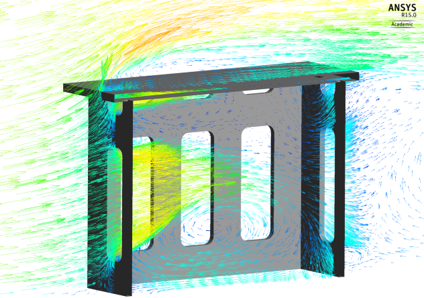
In forced convection heating (such as in an oven or autoclave), the configuration of the tool can significantly impact the airflow around the tool-part assembly. This, in turn, affects the local heat transfer coefficient, altering the heat transfer to and from the part. Specifically, the shape and substructure of the tool are major factors.

Schematic showing the effect tooling shape has on airflow and HTC values.

Schematic showing the increased toolside airflow for an open vs closed tooling substructure.

Shape

Airflow impinging on the tool is affected by local obtrusions which may redirect the air and create localized dead zones with their own convection currents. Similarly, large cavities in the tool can also create dead zones of little to no airflow. All of this affects the HTC across the tool which in turn affects heat transfer to the part. While for simple geometry it may be reasonable to assume a global heat transfer coefficient across the tooling surface, the same assumption cannot be made if the geometry is complex. Local variations in HTC should be investigated. In fact, if a convective heating system, such as an oven or autoclave, is loaded with multiple parts and tools, the same effect may be observed. That is, the airflow impinging on one tool-part assembly may be redirected in such a way that it affects the airflow on subsequent tools/parts. To overcome this, the heating system must be able to maintain a constant airflow stream across each tool-part assembly. This can be especially challenging if the tool-parts being loaded are not consistent in geometry or in their position within the heating system. The latter point can be combated by always loading equivalent tools/parts in the same position for each run.

Refer to the following pages for measuring airflow:

• How to measure airflow in a thermal system
• How to simulate airflow in a thermal system

Substructure

Tooling can generally be broken into two components. The facesheet (or skin), the upper section of tooling that supports and shape the part, and the substructure, the underside of the tool which provides support to the facesheet. The substructure can either be open or closed. Open, meaning air can easily flow through the underside of tool, versus closed where air cannot easily penetrate the underside of the tool. An example of open and closed substructures are shown.

Cross-sectional view of how tool sub-structure may block air flow in a simulation

An open substructure increases airflow under the tool, allowing for improved heat transfer and a higher HTC across the lower facesheet surface. A closed substructure, on the other hand, limits airflow, thus decreasing heat transfer and the HTC across the lower facesheet surface. For tools with a low thermal mass relative to the part, it is generally best to increase the toolside HTC. For tools with a high thermal mass relative to the part, the opposite is true, the toolside HTC should be decreased.

For tools with high thermal mass relative to the part, increasing the toolside HTC increases the maximum part temperature. The hold temperature in this scenario was 180°C.

If the thermal mass of the tool is high relative to the part, increasing the toolside HTC may increase the maximum part temperature. This may seen counterintuitive. The reason is that the higher the thermal mass of the tool, the longer it takes to heat up. If the thermal mass is considerable, then when the part exotherms the tool will still be "cold", allowing for the tool to absorb a considerable amount of the exothermic heat generated. Increasing the toolside HTC, however, decreases the heat up time of the tool, thereby allowing for a higher tool temperature when the part exotherms. This reduces the energy absorbing capacity of the tool during exotherm, thus raising the part temperature. In contrast, tools with a low thermal mass compared to the part exhibit a similar temperature to the part at the time of exotherm. Moreover, owing to their low thermal mass, they cannot absorb as much thermal energy as high thermal mass tool. As a result, is is more important to draw heat away from the tool in this case. This is achieved by increasing the toolside HTC.

Refer to equipment effects in a thermal management system to learn more about HTC effects.

Localized weld beads (for metallic tools) or pad-ups (for composite tools) can also affect the thermal uniformity of the tool. Weld beads refers to areas where the substructure is welded to the tool surface. Pad-ups are commonly used to meet tooling thickness, vacuum specifications and sometimes to accommodate inserts, location holes etc. These extra mass takes more energy and time to heat up and can lag areas on the tool without these features.

Effect of material

Thermal mass is the mass of an object multiplied by its specific heat capacity. Mass can be further represented by an object's volume multiplied by its density. Therefore thermal mass is both dependent on geometry (volume) and material properties (density and specific heat capacity). In the above section, increasing tooling thickness is shown as one way to increase a tool's thermal mass. Another is to change the tooling material to a more dense and/or higher specific heat capacity material. From a thermal management perspective, doing this serves the same purpose as increasing the tooling thickness. It will raise the tool's thermal mass and allow it to better act as a heat sink. If the process requires the tool to absorb a considerable amount of heat, this may be a good choice. However, if the process requires that the tool and/or part is highly responsive to changes in temperature, this may be a poor choice.

\(Q=mC_p\Delta{T}\) Energy required to raise an object's temperature, where:<br />\(Q\) = energy,<br />\(m\) = object mass,<br />\(C_p\) = specific heat capacity, and<br />\(\Delta{T}\) = change in temperature from applied energy<br /><br />Note that \(mC_p\) is the thermal mass of the object.

\(\alpha=\frac{k}{\rho C_p}\) Thermal diffusivity, where:<br />\(\alpha\) = thermal diffusivity,<br />\(k\) = thermal conductivity,<br />\(\rho\) = density, and<br />\(C_p\) = specific heat capacity

IR image showing non-uniform heating of a heavy invar tool with high thermal mass

Thermal mass is not the only factor that must be considered however. The tool's thermal conductivity and diffusivity play an important role. Thermal conductivity refers to how well the material transfers heat energy, while thermal diffusivity is a measure of the rate of this heat transfer, taking into account the object's conductivity and thermal mass. Thermal diffusivity is proportional to the thermal conductivity and inversely proportional to the specific heat capacity and density (related to thermal mass). In order for the tool to be an effective heat sink, it should have a high thermal conductivity. In that sense, it can easily draw heat from the environment and transfer it to the part, and vice versa. If the tool has both high thermal conductivity and is thermally massive, then it can not only readily transfer heat, but can also absorb a significant amount. If the thermal diffusivity of the material is also high, then heat can more easily dissipate through the material. What this means is that tools with high thermal diffusivities, such as aluminum, show more uniform temperature distributions. Tools with low thermal diffusivity tend to show more severe temperature gradients across their surface. Composite tools for example, have a generally low thermal diffusivity and also a low thermal mass. Therefore, they are subject to local temperature swings and may present significant difference in temperature across their surface. Their low thermal mass allows for them to heat up easily, but their low diffusivity does not allow for this heat to dissipate. On the other hand, while the diffusivity of invar and steel tools is still low compared to aluminum, it is much greater than that of most composite tools, and so too is their thermal mass. This means they take considerable energy to heat up but can dissipate that heat better than could a composite tool.

To see a practical example of these effects, refer to the tooling survey section below, which links out to a case study that demonstrates such phenomena. Quantitative values of physical and thermal material properties for tooling materials are provided in the table below, followed by a qualitative comparison of tooling materials.

Typical material properties for tools. Note that the properties for the composite tool are dependent on the fibre volume fraction and orientation.

Tooling material	Density (kg/m3)	Specific heat capacity (J/kg-K)	Thermal conductivity (W/m-K)	Coefficient of thermal expansion - CTE (x10-6/°C)	Thermal diffusivity (x10-6m2/s)
Invar	8000	515	11.0	0.6-1.5	2.67
Mild steel	7850	510	55	11	13.7
Carbon-epoxy composite	1580	870	0.7 (through-thickness)	-0.5 (in-plane) 22.5 (through-thickness)	0.5 (through-thickness)
Aluminum	2710	896	167	23	68.9

Qualitative comparison of tooling materials

Tooling material	Cost	Durability	Weight	Thermal mass	Thermal conductivity	Coefficient of thermal expansion (CTE)	Thermal diffusivity
Invar	$$$	Excellent	Heavy	High	Moderate	Low	Low
Steels	$$$	Excellent	Heavy	High	Good	Moderate	Moderate
Composites	$	Low	Light	Low	Low	Moderate	Low
Aluminum	$$	Good	Moderate	Low	Excellent	High	High

In the above figures (from the previous section), aluminum was used, which has a high thermal conductivity and high thermal diffusivity, but less thermally massive than steel or invar. Metals in general are good thermal conductors, therefore in the examples shown below, the increase in thermal mass associated with steel and invar tools translates to them being more effective heat sinks for part. In general, however, a composite tool is thermally light and has a lower thermal conductivity than the metals shown. Hence, the thermal response of the part is more exaggerated for a composite tool.

At room temperature, changing the material of the tool can significantly impact the part temperature during exotherm. With the glass-polyester system shown (left image below), changing from a 10mm composite tool to a 10mm invar tool reduces the maximum part temperature by 70°C. Although not as drastic, a similar response is seen at high temperature for a carbon-epoxy system (right image below). A 10mm composite tool results in a notable exotherm, 20°C above the environmental conditions. A 10mm steel and invar tool, on the other hand, reduce the part temperature overshoot to less than 10°C above the applied temperature.

Just as with thickness effects, a higher maximum temperature associated with a given tooling material results in a higher degree of cure for room temperature processing. Again, during high-temperature processing, however, the part eventually reaches the intended temperature regardless of the tool material. Therefore, the final degree of cure for each tooling material is the same; it is only the time in reaching the final DOC that differs. For both room and high-temperature processing, caution should be taken to avoid raising the part temperature above the material's degradation temperature.

Thermal response of two material systems on a 10mm tool of varying material. Left: Glass-polyester composite cured at room temperature (20°C). Right: Carbon-epoxy composite cured at 180°C with a ramp rate of 3°C/min in an oven.

Room temperature (20°C)	High temperature (3°C/min to 180°C)

The tool does not need to contain a single material (or thickness). In fact, realizing the use of the tool from a thermal perspective allows one to tailor its design to achieve the necessary properties. For example the tool assembly could comprise a thermally massive facesheet of invar (or steel), supported by a highly conductive block of aluminum to act as a heat sink. During heat up, the aluminum will readily conduct heat into the invar facesheet supporting the part. Similarly, during exotherm, the aluminum block will transfer heat away from the invar facesheet, thereby reducing excess heat given off by the part.

Aluminum block added under invar tool to act as an additional heat sink.

Fibre content (composite tool)

The thermal properties of composite tools are largely dependent on the volume fraction of fibre and resin, since the fibres and resin have different thermal properties. In the case of carbon fibre epoxies, the fibres are significantly better thermal conductors than the epoxy, while the specific heat capacity and density are fairly similar. Therefore the varying thermal response of CFRP tools is largely due to differences in thermal conductivity arising from their fibre volume fraction. A composite tool with a high fibre volume fraction will conduct heat much more readily than an equivalent tool with a low fibre volume fraction.

The anisotropic nature of composites also influences the thermal properties of composite tools, as they will have different properties depending on the fibre direction.

While metallic tools may be more rugged and can handle high temperature applications, composite tools are more sensitive. Aside from thermally degrading the composite part, it is also possible to thermally degrade a composite tool. As such, it is important that the tool also does not exceed its maximum temperature specifications.

Tooling survey

Understanding how the tooling parameters influence the thermal response of the part is important when designing and selecting tools. In addition to understanding the general effects that tooling may play, one can conduct a tooling survey to understand the specific thermal response of their individual tools. This means running tools through thermal cycles without the part present and measuring the temperature of the tool. This allows manufacturers to ascertain a better idea of how their tooling will behave during a production run. Of course, the thermal resistance and exothermic heat of the part is not captured in such a study. However, as explained in this page, the thermal response of the part is heavily influenced by the thermal response of the tool. Therefore, understanding how the tool behaves without the part is useful in understanding how the part will behave when placed on the tool.

The following link provides an example of a thermal tooling survey conducted on three complex tools having the same geometry but constructed of different materials. The results from this study demonstrate the applicability of the information presented in this page.

• Conducting a thermal tooling survey on three complex tools of different materials

Scenarios

1. A boat manufacturer is performing a room-temperature wet layup with a glass-polyester composite. The technical data sheet for the resin says the maximum processing temperature for the resin is 100°C. They are considering an aluminum or composite tool and wish to know what tooling thickness/material they should use to achieve the temperature specification while obtaining the highest DOC. As well, they would like to know the resulting gelation time.

In order to find the optimum tooling thickness to satisfy the temperature requirement, a thermal study must be performed on the tooling. It is assumed that the heat flow is one-dimensional. Using simulation software, the following curves are generated.

Downselecting a tooling material and thickness for a room temperature cure of a glass-polyester composite.

The figures show that under the given processing conditions the composite tool will never pass the temperature requirements. Therefore an aluminum tool is chosen. The minimum thickness needed to satisfy the temperature specification is ~12mm. The associated DOC for the 12mm aluminum tool is 0.96. However, for a small reduction in DOC, the manufacturer can select a 15mm tool which will bring the maximum part temperature down to 80°C. This will ensure that the part does not go above 100°C if unexpected, small temperature fluctuations occur. From the curves, a 15mm aluminum tool results in a DOC of ~0.94.

It is known that for this material system gelation occurs at a DOC of 0.1. Therefore gelation time can be deduced from a plot of DOC vs time for a 15mm aluminum tool

Degree of cure for a glass-polyester composite cured at room temperature on a 15mm aluminum tool. Gelation time for the composite was experimentally determined to occur at a DOC of 0.1

The gelation time of the resin in the system described above is approximately 116 minutes, or just under 2 hours, when cured at room temperature in stagnant air.

Complicating factors/edge cases

It should be noted that while this page demonstrates the general effects tooling has in a thermal system, the figures generated are material specific. Results will differ between materials, even for seemingly similar material systems (i.e. one polyester resin based system versus another). Similarly, changes in other processing parameters such as part thickness or HTC values will influence the outcomes. The results shown here are intended only to highlight the importance of tooling from a thermal management perspective. Finally, addition of consumables such as release film, breather, and vacuum bagging material were largely overlooked in the plots to simplify the explanation. Depending on the thermal properties and thickness of the consumables added, they may have a notable effect on the system. This is especially true for breather which can act as an insulator within a thermal system. The effect of consumables should be considered if a vacuum bag assembly is used.

Related pages

Page type	Links
Introduction to Composites Articles
Foundational Knowledge Articles
Foundational Knowledge Method Documents
Foundational Knowledge Worked Examples
Systems Knowledge Articles	Effect of equipment in a thermal management system - A110 Effect of material in a thermal management system - A155 Effect of shape in a thermal management system - A154 Effect of tooling in a thermal management system - A142
Systems Knowledge Method Documents
Systems Knowledge Worked Examples
Systems Catalogue Articles
Systems Catalogue Objects – Material
Systems Catalogue Objects – Shape
Systems Catalogue Objects – Tooling and consumables
Systems Catalogue Objects – Equipment
Practice Documents
Case Studies
Perspectives Articles	Introduction to Tooling for Composite Materials Processing - A340

References

References

About	Help

A central processing theme in the manufacturing cycle. This theme is concerned with managing the thermal response of materials during storage and handling or parts/tools when they are subsequently heated.

Degree of cure (DOC) is an indication of how far the chemical curing reaction (crosslinking process) has advanced in a thermoset resin.

DOC is defined with a number between 0 and 1 (or 0% and 100%) where 100% is a fully cured resin. It does not have to fully reach 100% for the resin to become solid or the part to be used. In some aerospace applications, resins are only cured to about 90%. Higher the degree of cure, higher the mechanical properties.

For polymer matrix composites (PMCs), resin refers to the matrix; the continuous material phase that binds the reinforcement together, maintains shape, and transfers load. Resins are divided into two main groups: thermosets and thermoplastics.

Engineered materials (designed to have specific properties) made from two or more constituent materials with different physical or chemical properties. The constituents remain separate and distinct on a macroscopic level within the finished structure.

Volume fraction of either matrix or fibres with respect to total composite volume (matrix + fibre).

Polymerization of thermoset resins is an exothermic reaction and heat is generated during the curing process. A thermosetting resin has the potential to release a certain amount of energy while curing. This is called the total heat of reaction, H_R, with a unit of J/g (SI units).

The heat of reaction during polymerization is measured using a Differential Scanning Calorimeter (DSC) equipment measuring much energy/heat comes out of the reaction for a small resin sample.

The use of multiphysics models to predict the outcome of real-world scenarios. May be analytical (closed form, "hand calculations") or computational (implementation on computers is required due to the large number of calculations involved. e.g. finite element method, finite difference method)

Most often in composite materials engineering, modelling refers to either:

• Process modelling (predicting manufacturing outcomes, or the inverse problem of predicting manufacturing parameters to achieve a desired outcome), or
• Performance modelling (predicting the stiffness/strength/suitability of a structure, or the inverse problem of the material properties and dimensional requirements to achieve a desired stiffness/strength/suitability of a structure)

(same as "Simulation")

The use of multiphysics models to predict the outcome of real-world scenarios. May be analytical (closed form, "hand calculations") or computational (implementation on computers is required due to the large number of calculations involved. e.g. finite element method, finite difference method)

Most often in composite materials engineering, simulation refers to either:

• Process simulation (predicting manufacturing outcomes, or the inverse problem of predicting manufacturing parameters to achieve a desired outcome), or
• Performance simulation (predicting the stiffness/strength/suitability of a structure, or the inverse problem of the material properties and dimensional requirements to achieve a desired stiffness/strength/suitability of a structure)

(same as "Modelling")

A quantitative measure of how a material will respond to transient thermal conditions. It is defined as the ratio of thermal conductivity to the volumetric heat capacity of the material (density times the specific heat capacity).

Materials with large thermal diffusivity have a high thermal conductivity relative to their capacity to store energy (heat capacity) and will rapidly distribute the thermal energy throughout its volume and rapidly change temperature to reach the new equilibrium temperature.

Materials with small thermal diffusivity have a low thermal conductivity relative to their capacity to store energy (heat capacity) and will have a sluggish temperature response to a change in thermal conditions (large temperature lag). This is because it takes more energy per unit volume to change the temperature, and the low thermal conductivity means it takes longer to distribute the thermal energy throughout its volume.

Carbon fibres are composed of large aromatic sheets similar to those in graphite. These graphitic layers form the basic structural units in the shape of ribbons. The structure of carbon fibre ribbon is believed to be a columnar arrangement of disoriented graphite crystallites parallel to the ribbon length. The idealized tetragonal crystallites are stacked above one another, with slight disorientation between the crystals in the direction of fibre axis, trapping sharp needle like voids, where the boundaries between the stacks represent the disordered regions.